Explaining Professor Alan Nathan’s Optimal Swing Theory and how it Morphed into an Inefficient Swing Philosophy
By Ken Cherryhomes ©2025
Introduction
Today, too many analytics are focused on outcome, but not the methods or means to achieve or improve upon them. A hitting paradigm has been built on sound science, but is this science being interpreted and applied incorrectly, and are hitters suffering the consequences as a result of the inefficiencies of the methods aimed at achieving specific objectives?
I’ll begin by saying, I agree with Professor Alan Nathan’s conclusions. His work identifying the optimal attack angle for achieving optimal launch angle for maximum launch distance is 100 percent valid. In a vacuum.
But outside that vacuum there is something equally as important: how to arrive at that optimal attack angle. The movement that produces the outcome—the means—needs to be addressed. Ignoring this in favor of outcome metrics alone distorts the swing.
The moment one variable is declared optimal, the process often gets reversed. Coaches, and players, start reshaping the swing to match a theoretical result, rather than asking whether the result can be achieved through a more efficient or natural method.
Nathan’s study accomplished exactly what it set out to do. It modeled the best way to produce a specific outcome—maximum flight distance—under controlled conditions. But the study wasn’t designed to account for biomechanics, time constraints, or pitch variability. That wasn’t its job.
This article doesn’t pick up where Nathan’s study left off. It exposes where it failed to begin. I’ll reintroduce the parameters his model ignored, the ones that matter when the pitch is moving, and the swing is real. What followed his work wasn’t scientific advancement, it was a hijacking. One narrow, lab-defined variable was declared optimal, and everything else—mechanics, timing, efficiency—was bent around it. The result is a generation of hitters taught to chase outcomes through inefficient, overengineered movements, all in service of a model that never once asked how the swing would be performed.
Professor Nathan’s Study
Professor Nathan’s study, “Optimizing the Swing”, was published in The Hardball Times on November 11, 2015. The study was precise and narrow in scope: maximizing flight distance under fixed conditions.
I’ll include his original diagram and a paraphrased explanation. Like many physics papers, it was presented as simplified for non-physicists, though it still manages to tie itself in knots. So, I’ll lay out the model in plain terms.
Test Setup
- The ball is placed on a tee, three feet off the ground.
- It’s positioned at the front-middle of the plate, aligned with second base and center field.
- The bat is swung at a fixed speed of 70 miles per hour.
- The goal is to hit the ball directly to center field.
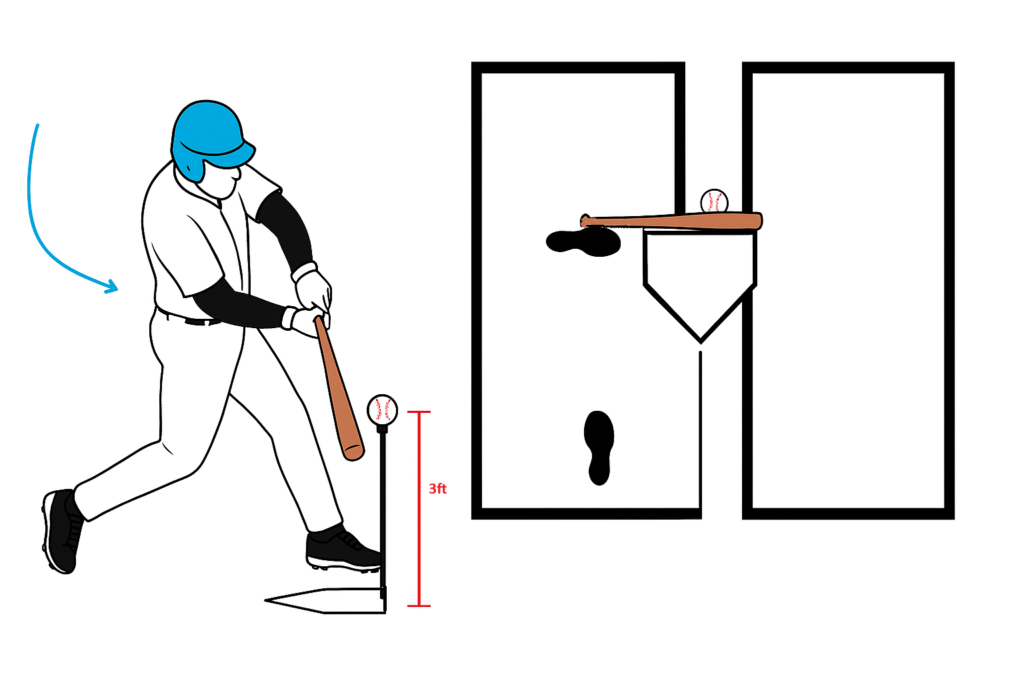
Whether this was a thought experiment or involved actual physical testing isn’t clear. It doesn’t matter. The point of the model was to define the geometric and physical conditions under which a ball will travel the farthest. And under these conditions, Nathan arrived at a specific conclusion: a bat traveling upward, at a specific instantaneous collision angle to the pitch’s descent angle, with a precise offset, produces the optimal launch angle and exit velocity for maximum launch distance.
But let’s not skip over something subtle: just because the ball is over the middle of the plate doesn’t mean hitting it guarantees a shot to center field. That depends entirely on a specific set of parameters: the hitter’s orientation in the box, physical proximity to the ball, direction of their swing, and the orientation of the barrel at contact.
For the ball to be driven to dead center with maximum efficiency, the barrel must strike it square, with the sweet spot arriving perpendicular to the ball’s path. That level of precision depends on the hitter’s orientation in the box, the swing’s directional intent, and the spatial relationship between the bat and the ball at contact. When those align, the result is a clean, efficient transfer of energy, sending the ball on a straight line to center.
This might sound like unnecessary detail, but it’s not. It matters later—when we stop analyzing theoretical collisions and start dealing with the biomechanics required to make them happen.
Professor Nathan’s Optimal Attack Angle
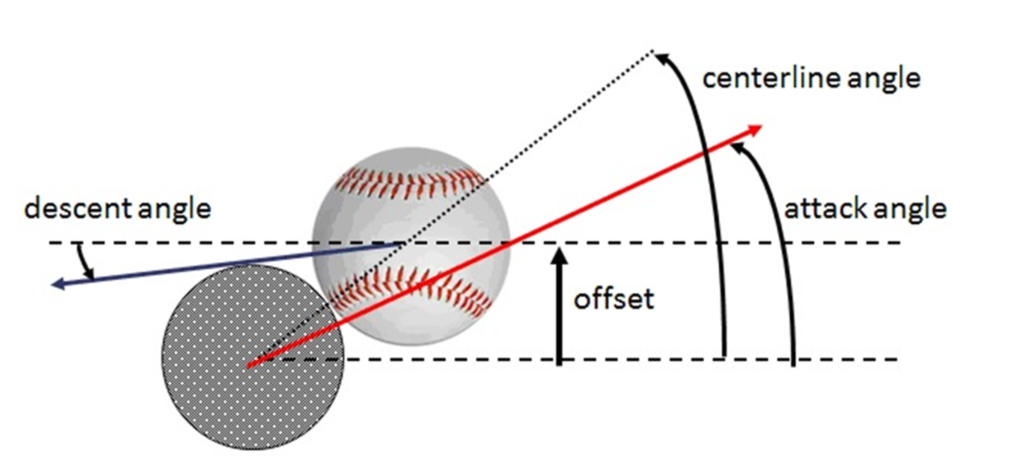
Below is Professor Alan Nathan’s diagram illustrating the geometric relationships that define his swing optimization model.

In this model:
- The centerline angle is the dotted line connecting the bat’s center to the center of the ball. It defines the directional vector of energy transfer.
- The offset is the vertical distance between the bat’s centerline and the ball’s center at contact. This is a semi-controllable variable—essentially a measure of where the bat is aimed.
- Attack angle refers to the bat’s orientation at the moment of contact, not to be confused with swing path.
- The descent angle is the incoming trajectory of the pitch.
Nathan’s core conclusion is simple: if your goal is to hit the ball as far as possible, then swinging downward, creating a negative attack angle that opposes the pitch’s descent, does not appear to be a good idea. In other words, match the swing plane to the pitch plane.
That claim holds if we assume a swing path with no curvature, and no influence from human mechanics. But that’s a flawed assumption.
As a hitting coach, I initially had a hard time accepting the idea that a bat traveling upward into a pitch designed to fly to centerfield was the optimal approach. Not because the math was wrong, but because my definition of optimal includes more than just trajectory and speed, it includes swing efficiency, margin for error, time to execute, and biomechanical cost.
But sticking strictly to the physics, Nathan’s conclusion was based on a single, instantaneous event: bat meets ball. It doesn’t address how that orientation is achieved or what tradeoffs are required to get there. It isolates the moment of contact, not the movement leading into it.
That led me to the core question: if two bats strike the same ball at the same speed and at the same point—one coming from above and arcing to level, the other coming from below and maintaining its upward path—how does the upward-moving bat create more distance and more efficiency at the same time?
From a biomechanics standpoint, it doesn’t. A swing that begins above the ball and arcs naturally to or through the plane of contact is not only more intuitive, it’s more stable. It’s hand/eye friendly, less prone to offset errors, and more mechanically efficient. The upward swing, by contrast, requires early commitment and maintains vulnerability to timing miss or spatial deviation.
And that raises another issue: the myth of “being on plane.” If a pitch is descending at 6 degrees and the swing is ascending at 18 degrees, then you’re not on the same plane. You’re crossing it—just like a downward arc that levels off and continues. There’s no greater overlap, no increased margin of error, and no meaningful plane match. What’s being sold as optimization is really just intersection at a single point, and that’s not the same thing.
I already understood what contributes to ball flight. Exit velocity is a function of bat speed and bat weight. Launch angle, on the other hand, can be manipulated through offset, independent of attack angle. With a round bat striking a round ball, meeting the ball below its center produces an upward launch angle. You don’t need an upward swing path to produce an upward ball flight. That’s a key distinction most people miss.
So, when I saw the conclusions drawn from Nathan’s model, I didn’t question the outcome. I questioned the assumption that altering swing direction was the only—or even the best—way to achieve it.
The Flawed Setup: Why Center Field Fails as a Standard
There’s another layer to this most people miss. Every swing, regardless of style, will pass through an “optimal” attack angle—say, 18 degrees—somewhere along its arc. But when and where that happens depends entirely on pitch location, contact depth, and timing. The swing doesn’t begin at that angle. It passes through it—often out front, particularly on inside pitches, where the barrel is naturally accelerating and ascending.
That’s precisely why the test conditions used in Nathan’s study matter. The model fixed the pitch location over the middle of the plate and assumed a ball driven to centerfield. But that location is not where the bat reaches peak velocity, nor where the arc has naturally begun to rise. In real swings, the highest bat speed occurs out front—on pull-side contact—where angular momentum and energy transfer peak.
Nathan’s model, by fixing swing speed, eliminated this natural peak-speed zone from the equation. That was necessary for isolating variables, but it created a distortion: 18 degrees emerged as optimal not because it reflects the longest possible hit, but because the longest possible hit—the one out front with greater bat speed—was excluded from the model.
That misinterpretation metastasized. Instead of treating 18 degrees as a fleeting orientation along the arc, coaches and players began engineering swing paths to arrive at 18 degrees, regardless of pitch type, location, or context. It became the destination, not a point passed through. A constraint of the model became a constraint on the swing.
The result was a movement system retrofitted to satisfy a number. The swing no longer adapted to pitch conditions. It was fixed, rigid, built to chase an angle that only made sense in a physics simulation with a frozen bat.
Even if everything else were equal—bat speed, offset, descent angle—centerfield is structurally disadvantaged. It’s not where you reach peak bat speed, and it’s not where a mistimed swing is most forgiving. Slight mis-hits to center die. Slight mis-hits pulled go out. The field doesn’t play neutral, and the experiment shouldn’t pretend it does.
So, what looked like an elegant optimization in theory became an impractical prescription in practice. A number derived from a fixed-speed, middle-location, centerfield-targeted model was treated as a universal truth —folded into a swing ideology.
Even under controlled conditions, outcomes are highly sensitive to offset. Below are three identical pitch scenarios—all at 6 degrees descent, with zero offset, and equal swing speed. The only variable is attack angle. The outcomes diverge dramatically.
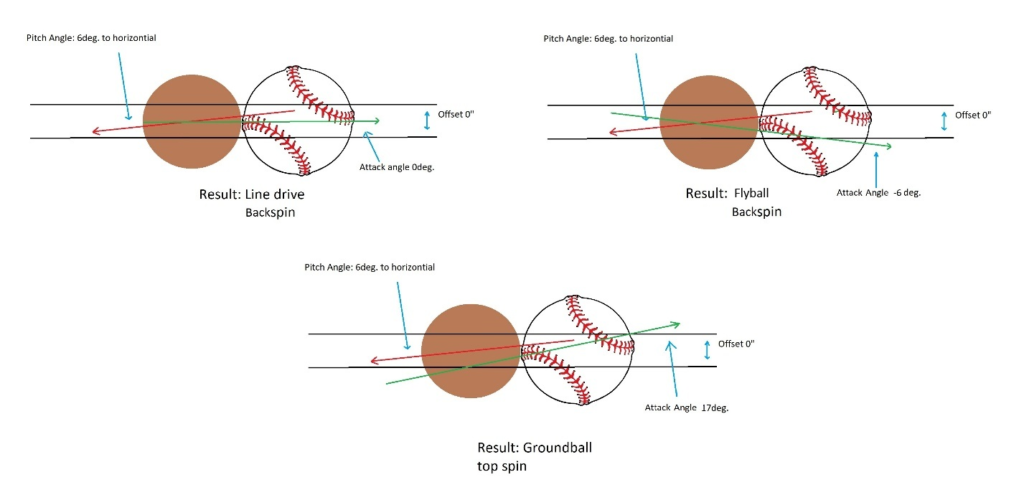
The takeaway here is simple: even when conditions are controlled and constant, the theoretical advantage of a steep attack angle collapses without precise offset. In live at-bats, that precision isn’t just difficult, it’s unrealistic. And chasing it often leads to more unintended, in-optimal outcomes than it prevents.
The Misuse of Good Science: How the Attack Angle Model Went Off Track
Now that we understand how Professor Nathan arrived at his conclusions, what matters now is how those conclusions have been interpreted, and more importantly, how they’ve been implemented.
Numbers don’t lie, but the way we use them can. In today’s game, conclusions supported by science quickly become dogma if they support a narrative. For the quantitative analyst, the game of baseball begins after it’s played. But that postmortem rarely includes the behavior, decisions, or physical tradeoffs that shaped the outcome.
The Misinterpretation of Optimal: How a Physics Model Became a Swing Philosophy
As a hitting coach and lifelong student of the game, I’ve always respected the role of analytics. Baseball is a high-stakes sport. Outcomes matter. Exit velocity, hard-hit rate, on-base percentage—these aren’t just abstract metrics. They reflect what happened and, often, what’s likely to happen again. My job has always been to help hitters improve those outcomes without compromising the swing itself.
But what analytics often fail to answer is how. How do you build the swing that produces those metrics—without sacrificing adaptability, timing, or efficiency?
The rise of the attack angle focused swing is a perfect case study in this failure. It was hailed as the mechanical key to unlocking optimal launch angle, itself considered the Holy Grail of modern hitting. Professor Nathan’s study was invoked as proof. His physics-based model showed that a ball struck at a certain upward attack angle, with a certain, though highly sensitive offset, produces ideal carry and maximum flight distance.
And statistically, that result held up. Balls hit in the air were more productive than ground balls, even if they occurred less frequently. The conclusion? Swing upward. Produce the right attack angle, and the results will follow.
But what the model didn’t offer—what it never set out to offer—was implementation. Nathan’s study was theoretical by design. Nathan’s model was never meant to prescribe mechanics or training methods—it defined an optimized contact moment, not the path to it. And yet, entire training systems were built on it.

What followed was predictable: drills aimed at manufacturing upward attack angles started flooding swing content platforms. The movements were often forced, indirect, or biomechanically inefficient—but they fed the metric. So, hitters built their mechanics to chase it.
And it showed. A generation of hitters started arriving with long, looping uppercuts—not powerful arcs, but engineered movements. Notably, these swings weren’t intuitive. They weren’t explosive in the way Albert Pujols’ “swinging down” path is, Pujols being one of the best in the world at matching intent with efficiency in measures of both power and consistency. These were constraint-based swings, designed around a number rather than an outcome.
I saw it most clearly in hitters like Cody Bellinger. An elite talent whose raw tools were undeniable, but whose production, in my opinion, suffered under the weight of a less than optimal swing theory. Applying the same steep path to every pitch type and every location isn’t a philosophy—it’s a limitation.
And that’s the problem. Numbers don’t lie, but they don’t teach either. They describe, not prescribe. What followed was a wholesale misinterpretation of his work—a mechanical philosophy built on an outcome that wasn’t meant to dictate the path to it.
This article is about that path.
What follows is not a refutation of the physics, but a correction to the implementation. I’ll show how to achieve optimal launch angles—and even the coveted attack angle—through the most efficient means possible. A means that accounts for time, repeatability, natural execution, and mechanical integrity. Because optimal isn’t just about the longest ball flight—it’s about the most sustainable way to hit.
Swing Paths and Efficiency
Efficiency is the core of how I define optimal. That doesn’t just mean ideal result, it means ease of execution, consistency in achieving the objective, and since we’re dealing with moving pitches under time constraints, time of swing execution (how long it takes to swing) as well.
In baseball, there are three primary swing path types commonly taught or practiced:
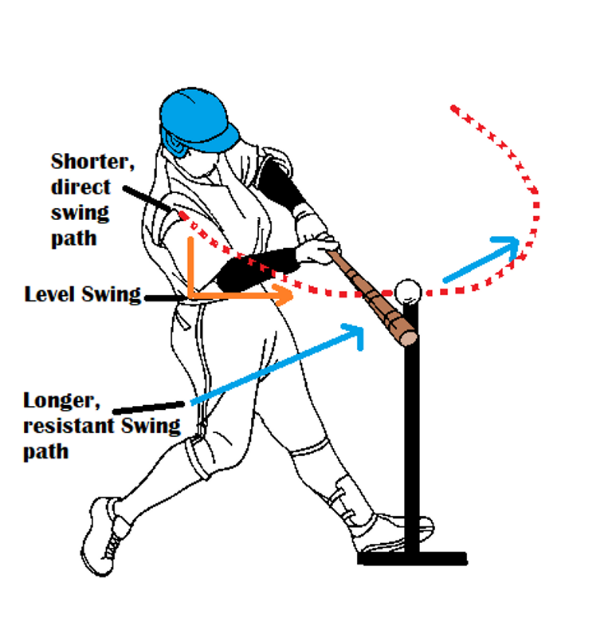
- The “natural” swing, often mislabeled the “downward” swing
- The level swing, a flat, horizontal path intended to match pitch plane
- The uppercut swing, now rebranded as the “attack angle swing”
Each has its theory, and each makes different tradeoffs. Let’s go through them.
The “Natural” Down and Through Swing

The so-called “down” swing isn’t truly downward in its intent or outcome. It’s better understood as a natural, arcing motion—a direct path to the ball that flows from the hitter’s natural hand position, typically above the zone, toward the targeted point of contact.
To define what I mean by “natural,” imagine you’re reaching for a glass of water that’s one foot below and one foot in front of your chest. You don’t drop your hand to its height and then extend outward in a straight line—you follow a natural arc, a diagonal, efficient movement. It’s direct, logical and intuitive. The same principle governs the bat path.
The natural swing follows a sequence: down and forward, then level and forward, then up and through—similar to the arc of a playground swing, though not as exaggerated. Once launched with intent, beyond directional guidance, the bat doesn’t require further assistance to keep moving. It’s momentum efficient, time efficient, and biomechanically intuitive. And most importantly, it’s adaptable. Line drives, home runs, and ground balls can all result from it, depending on timing, pitch location, barrel transition at point of contact (descending to ascending and in-between), and barrel/ball offset.
The only time a “downward” swing yields a negative attack angle is when the swing is late—catching the ball too deep and early in its arc—or when the downward path is exaggerated by a forward shift in the batter’s center of mass, tipping them off-axis and extending the downward portion of the arc.
Another key benefit: it doesn’t have to be taught. You can see it in toddlers who have intuitively solved the first order constraint—intersection timing—before coaches intervene with theory or instruction.

The eyes direct the hands. The hands move the bat. Unless the hitter disrupts the process by attempting to control the act, the motion happens naturally. And with proper timing, that same swing works against a moving pitch just as well as it does on a tee.
Where confusion often enters is in how this motion is visually interpreted, especially when discussing “feel versus real.” What’s often missed is that while the hands chart a mostly linear path forward—efficient and direct—the barrel appears to move on a more pronounced arc. This visual cue has misled many into thinking the hands are swinging downward in a curved path when, in reality, the arc results from wrist articulation. At launch, the barrel begins well above the hands, and as the hands move forward, the wrists naturally lower the barrel into the path of the pitch or below the pitch, depending on the outcome intent. Depending on pitch height, this adjustment can be more or less pronounced, giving the illusion of a loop. It’s not a random drop. It’s the brain’s grasping mechanism solving for contact. The hands don’t dive, the wrists articulate. That’s proprioception, not manipulation. And when left alone, that system is remarkably efficient.
The Level Swing
The level swing concept emerged from a desire to control and produce an outcome: the line drive. The goal was to match the bat’s path to the pitch’s trajectory and produce flush contact. On paper, the logic tracks. Line drives, while the least frequent batted ball type in MLB, yield hits nearly 70% of the time—compared to 24% for ground balls and 21% for fly balls.
But in practice, the interpretation goes sideways. To align the bat with the pitch plane, many hitters were either taught to, or instinctively began to, drop their hands to the height of the ball before initiating forward movement. The result was a bat path shaped like an “L”— first down, then forward.
That shape demands constant effort. Lowered hands eliminate stored energy, forcing the hitter to manually push the bat forward, resisting natural sequencing. This effort recruits the torso and chest, pulling the head and barrel off path.
Mechanically, it forms a rigid system: bat, arms, and chest move as a single unit. At full extension, the barrel may be pointed toward the dugout, with the hitter pulled off-axis. Contact is still possible, but the swing is time-inefficient, lacks torque, resists natural acceleration, and struggles to generate speed. And once the chain breaks down, outcomes become random—less consistent, less repeatable.
It is neither natural nor efficient.
The Uppercut, Attack Angle (“Launch Angle”) Targeted Swing

The uppercut swing has always had surface appeal. Even kids learn early: get under the ball, and it goes far. But what works by accident at 40 mph breaks down at velocity. The modern version of this swing—what’s now called colloquially the launch angle swing—isn’t just an exaggerated uppercut. It’s an engineered path built around a number: 18 degrees. That figure, drawn from Alan Nathan’s physics model, is treated as the hard science behind launch distance. But what’s missing in the translation is everything else: time, biomechanics, and context.
An attack angle is an instantaneous measure—a snapshot of the bat’s orientation at the moment of contact. A swing, on the other hand, is a sequence. When you design a full-body movement to satisfy a single frame in time, you’ve inverted the problem. You’re no longer trying to make solid contact—you’re trying to place a number on a graph.
To achieve that steep upward angle, hitters are coached into a set of compensations. The most common is a rear shoulder drop at launch. This tilts the upper body and forces a path that ascends early and stays steep. But unlike a downward, more natural arc swing that is aided by gravity, this path fights it. There is no external force assisting acceleration—only resistance. Because this path doesn’t self-reinforce, hitters must sustain effort throughout, replacing momentum with strain. That extra effort doesn’t stay isolated. It ripples outward.
To sustain momentum on a path that doesn’t self-reinforce, hitters turn to the chest, opening prematurely because of the sustained effort required to drive the barrel forward. But that compensation introduces a cascade: energy bleeds sideways, the head pulls, and the barrel travels blind. The effort applied to sustain the swing often redirects energy inefficiently, misaligning it with the incoming pitch. The result isn’t power—it’s instability.
Consider Cody Bellinger. In 2019, he won the National League MVP and led all of Major League Baseball in batting average against curveballs. The ball dropping perfectly aligned with his below the ball uppercut swing. His home runs were frequent, but often lacked the distance to match his perceived effort.
But after that season, his numbers began to collapse. I believe much of that decline was due to the same issue discussed here: a steep swing angle and efforted path that couldn’t hold up under timing pressure or plane alignment. The swing looked powerful, but it was inflexible—built around outcome, not adaptability.

One flawed movement requires another to keep the system from collapsing.
What results is a swing that is longer, less stable, and incredibly sensitive to both timing and spatial error. A clean hit can carry. But a near miss? That’s a weak fly ball or a topspin roller. The margin is razor thin, because the path is steep and the zone of effective contact is narrow.
And the biggest casualty? Line drives.
An 18-degree or any steep swing attack angle doesn’t cross the pitch plane in a way that supports backspin at a line drive trajectory. With as little as ½” error in offset, the collision either slides under, lifting the ball too steeply or glances over the top and top spins it. Both reduce the probability of a hit. And in trying to chase launch, hitters are systematically eliminating the one batted ball type that produces the most value.
Ironically, what this swing was designed to avoid—ground balls—has actually increased. Since the rise of the launch angle paradigm, Statcast data shows an uptick in ground ball rates across the league. Not because hitters are trying to hit down on the ball, but because steep swings with narrow margins create weak contact in both directions. One miss produces a pop-up. The other, a grounder.
What this swing claims to optimize, it actually erodes.
Misplaced Priorities: When Outcome Becomes the Definition of Optimal
Physics models like those identifying an optimal attack angle for optimal launch angle and batted ball flight distance offer a clean benchmark. But real pitches move. Timing windows collapse. Swings aren’t snapshots—they’re sequences governed by time, space, and consequence.
And this is where the priorities fall apart.
“Optimal” has been defined by result—exit velocity, launch angle, flight distance. But those are second-order outcomes. The first-order constraint in hitting is timing. It’s pitch-dependent, location-dependent, and must be solved before any mechanical intent or optimization can even begin.
When you build swing design backward—from result instead of constraint—you engineer inefficiency. You create movement patterns that might check the box of a physics model, but break under pressure because they ignore the one thing no hitter can avoid: time.
Let’s look at what that actually costs.
Swing Path Cost and the Illusion of Efficiency
Nathan’s model uses several fixed assumptions that are fair constraints for a physics problem, but in real hitting, swing path comes at a price.
Steep paths fight gravity and drain energy. Unlike natural arcs, they don’t accelerate efficiently, and that inefficiency ripples outward.
The swing becomes less about sequencing and more about compensation. To hold the barrel on a steep path, hitters engage muscles that should be secondary. The result isn’t added force—it’s energy misdirection. That loss doesn’t just show up in effort. It shows up in timing, in adjustability, in the body’s ability to repeat the movement under pressure.
That’s the real cost: not just more energy spent, but less energy available for correction. A swing designed to hold a line often loses the ability to make an adjustment. And in baseball, where the problem changes pitch to pitch, that rigidity becomes a liability.
Consistency: The First Casualty of Misaligned Design
First order principle theory suggests a swing philosophy should start with solving for a first order constraint: timing. Instead, most of today’s swing theory starts with a desired outcome and attempts to build the swing backwards from there; a second order problem centered on intent.
That inversion creates problems.
The natural arc adapts, resulting in direct, efficient swing paths. It allows for contact variability—early or late, up or down—while still producing competitive outcomes: line drives, fly balls, or hard grounders. The launch angle swing is far more precise. It relies on matching a narrow offset window and fixed path. Miss that window and you don’t just miss the ball—you miss the right type of contact.
That’s a critical issue. Because line drives aren’t just productive, they’re the most productive contact type in the game. Nearly 70% of them result in hits.
What’s often misunderstood is that a more natural path swing that makes flush contact—where the center of the barrel meets the center of the ball—results in a line drive. Shift that offset just slightly below center, and that line drive lifts for extra bases. A little more, and it’s a home run. All from a minimal, natural shift in offset.
When your swing path is already ascending steeply, small changes in offset don’t broaden your outcomes—they restrict them. The sweet spot collapses down to about an inch of vertical window. This is something I measured and published: a 1/2” change in offset produced drastically different outcomes on a steep path. That’s not a high-performance swing—it’s a risk profile.
So, while a swing built for attack angle might raise your launch angle on a perfect hit, it also systematically reduces the chance of the most reliable hit in baseball.
And that brings us back to the original problem: when you engineer a swing to serve intent before solving for timing, you break the very thing that makes offense repeatable.
Optimization Must Start With the Constraint
This isn’t about which swing path looks best in a lab. It’s about which one holds up under pressure.
An attack angle-targeted, steep swing path might produce more distance in a perfectly timed, perfectly offset collision. But that’s not how hitting works. Every pitch is a problem to be solved. If your swing isn’t built to solve problems, but only to produce narrow, idealized outcomes, it’s not built to last.
Optimization begins only after you’ve addressed the first order constraint: the thing that must be solved before anything else can be applied. In hitting, that constraint is timing.
Not intent. Not outcome. Timing.
Solve for that, and swing design becomes adaptable. Outcomes follow. And the game returns to the hitter, not the model.
Location, Leverage, and the Misapplication of Theory
It’s no surprise that Professor Alan Nathan, a Red Sox fan and admirer of Ted Williams, would be the physicist whose model of optimal attack angle appeared to have reverse-engineered the swing behind one of the most iconic hitters in baseball history. Nathan’s model reflects something Williams often emphasized: that swinging slightly upward—ascending through the ball—can produce optimal contact. But even that principle has been misapplied.
Williams advocated for swinging “slightly up” and for matching the plane of the pitch. But his swing mechanics, visible in archived footage and illustrated in his own book, don’t reflect a true match-plane approach. His barrel doesn’t trace the path of the pitch. Instead, the bat drops below the ball and rises into it on a forward-timed arc. His contact point is out front, and his barrel works from a descending launch to an ascending collision.

Williams succeeded by pulling inner-third pitches with explosive, forward-timed contact. But over time, the interpretation of his somewhat confusing guidance has drifted. “Swing slightly up” became “match the plane,” and “match the plane” became “swing along the pitch” and then swing at the optimal attack angle from the outset of the swing’s launch. That evolution redefined his original claim into a model of universal application, ignoring that his success was pitch-location dependent. And misunderstanding that distinction is how theory became dogma—and how optimization turned into overreach. Furthermore, with an average pitch descent of 6-degrees and a steep upward swing never matching planes, further confounds the logic of plane matching.

Not only are Williams and Griffey swinging below the pitch plane, targeting a forward contact point where the bat is naturally ascending at the end of its arc, neither exhibits the exaggerated shoulder drop or pre-tilted posture common in today’s attack angle and launch angle focused swings. Their swings weren’t built to satisfy a metric. They were built intuitively, over time, to fulfill intent. What they shared wasn’t a philosophy—they shared results rooted in adaptability, not engineering.
The Real Geometry of Pulling
I’ve taught every hitter I’ve trained to pull the ball properly—not by spinning off, not by guessing early, but by using the natural arc of the swing to let the barrel whip under and through. On middle pitches, when timed right, a natural swing sends the ball up the middle, slightly lifted with backspin. Want to increase the probability of a good offset? Use a smaller barrel. The narrower the barrel, the less flush the collision, the more likely you are to meet the ball below center.
On inside pitches, pulling isn’t just efficient—it’s biomechanically optimal. You’re meeting the ball where the bat accelerates the most, where centrifugal force is peaking. You don’t need to manufacture a swing plane to match the pitch. You let the swing’s arc do the work, and if you do it correctly, the bat naturally meets the ball on the way up, at precisely the moment Professor Nathan’s model says is optimal.
That’s what pulling properly looks like.
But the reason most hitters don’t pull well, and why it’s been demonized for decades, is because it confounds our instincts. Once the bat begins to arc below the ball, the brain sends a panic signal: you’re off course. Hitters instinctively “correct” mid-swing, locking up the front arm, flattening the barrel, and rolling over. It looks like a chicken wing. It ends in a ground ball to short or third base.
That’s not a mechanical failure. That’s a failure of perception, one that only gets worse when you try to overlay a rigid attack angle approach on top of it.
Pulling properly is either learned or accidental. Williams, Bonds, Griffey, McGwire—these weren’t hitters guessing early. They were hitters who had mastered the arc. They didn’t need to drop into a steep posture or engineer a mechanical tilt. They swung below the plane of the pitch, then let physics take care of the swing’s ascent. And the result was power, consistency, and control.
But it’s a difficult move to teach. Most coaches don’t teach it because they don’t understand it. And so, we build workarounds. Swing up early. Create lift. Manufacture an angle. Then wonder why whiff rates go up and timing windows shrink
Field Dimensions Aren’t Neutral—They Reflect Execution Probability, Not Physical Strength
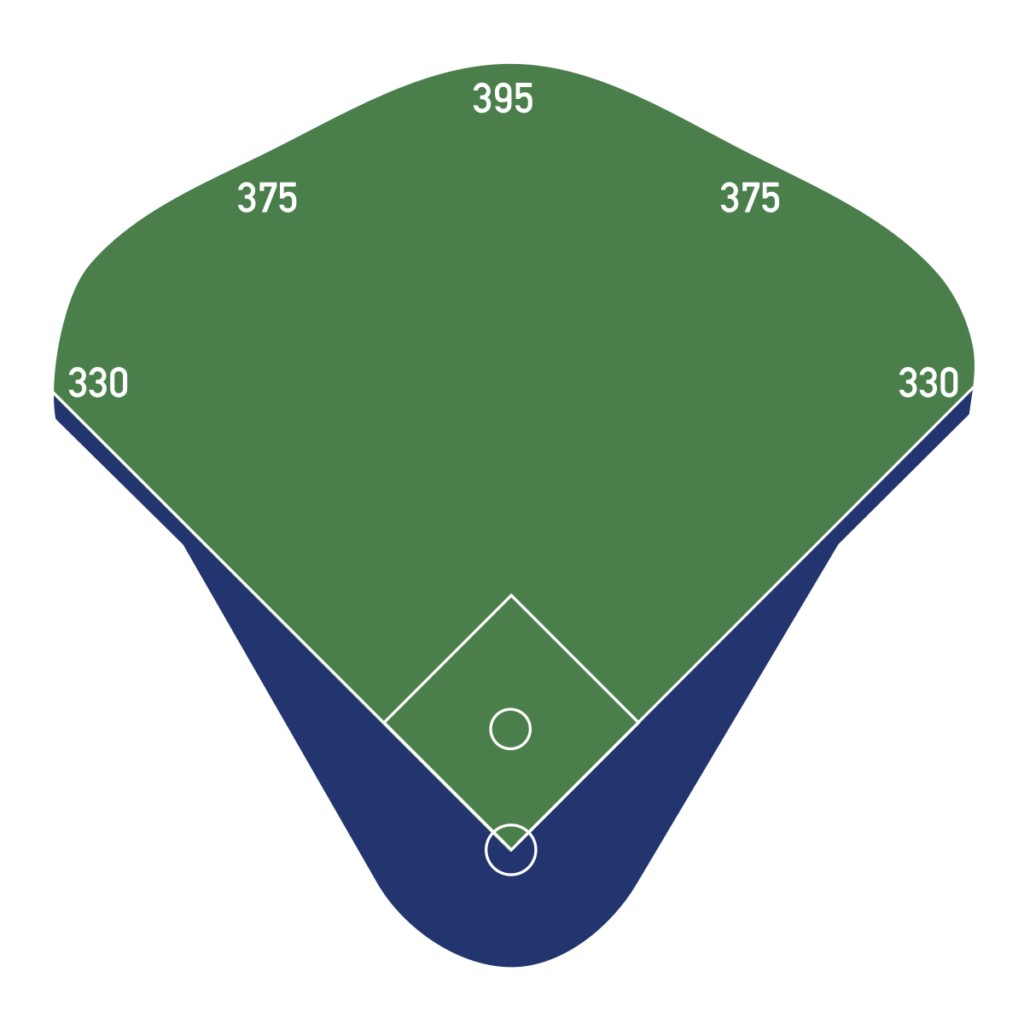
The field is asymmetrical by design. The shortest path to a home run is to the pull side. That’s not a coincidence. It may just happen to be where the barrel accelerates fastest, but it’s also where the most difficult swing to execute resides. Field dimensions don’t reward physical advantages. They reflect ease and difficulty of execution. Pull fields are shorter not because of where the barrel is fastest, but in spite of it.
Pull side swings are biomechanically explosive. The bat reaches peak acceleration out front, and when timed correctly, it delivers maximum force. But the shorter fence down the line doesn’t exist to reward that strength. It exists because that swing is the hardest to execute. Pulling with lift is generally limited to a narrow set of pitch locations, usually inside or middle in. It’s powerful, but it’s also rare. The reward of shorter pull side fences exists to balance the difficulty.
Center field reflects the opposite. Most pitch locations can be driven up the middle. The arc is natural. The timing is forgiving. A slight miss still produces a playable result. That’s why the wall stretches back. Not because center is the best place to hit, but because it’s the easiest to reach.
When a hitter pulls a pitch properly, with lift and intent, it takes full advantage of the body’s peak output. That’s the rare swing. That’s the one the field was shaped around.
That’s the part most ignore. Ballparks are shaped by the probability of outcomes, not just by raw strength. And that’s also why teaching hitters to pull properly—with lift, intent, and arc—isn’t about chasing power. It’s about leveraging the swing that, when executed well, is the most rewarded in the game.
Everyone in the big leagues can hit a ball 350 feet. To center, that’s a routine flyout. But when pulled in the air, that same 350-foot ball clears the fence in almost every park. That’s not just about distance. It’s about geometry. Pull fields are more forgiving—launch angle tolerances are wider, and the physical reward comes easier for the same output. Field dimensions don’t reward strength. They reward execution ease and commonality, and the margins built into the design reflect that.
Conclusion
I understand what Professor Nathan means by optimal attack angle. I understand what Ted Williams meant by a slightly upward swing and that it has to do more with point of contact and an ascending arc rather than chasing a steep attack angle metric. But when we start labeling any result as “optimal,” we owe it a disclaimer.
Optimal isn’t about the longest ball flight—it’s about consistency, repeatability, and results across timing windows. It has to account for the swing’s tolerance to timing and offset variation—because those are constants in real hitting.
With a line drive approach, if the hitter misses just below center, it might be a double or a home run. Miss just above, and it’s a hard ground ball—still a playable outcome. But with the steep attack angle swings, as they’re often applied today, it’s all or nothing. Miss underneath? That’s a pop-up. Miss early? That’s a topspin roller. The margin collapses.
The swing that stays fast, stays under control, and doesn’t need to be shelved with two strikes—that’s the one that holds up.
Broaden your zone with two strikes if you need to, but don’t slow your bat down. And if your two-strike swing looks nothing like your no-strike swing, maybe your no-strike swing was never built to survive in the first place.