In Pursuit of the Optimal Swing
By Ken Cherryhomes
Introduction
I will begin this study and discussion by stating, I absolutely agree with Professor Nathan’s conclusions for optimal attack angle for optimal launch angle to achieve maximum flight distance of a batted ball. This statement, on its own, requires a great deal of explanation. In all actuality, maximum flight distance occurs when a ball is hit to a pull field. Furthermore, by taking a downward swing path, optimal attack angle can be achieved. But that is for another discussion.
In his article, published by Hard Ball Times (November 11, 2015) titled, “Optimizing the Swing”, he includes his diagrams and explanations supporting his conclusions. I joked with him about his title, saying, at first glance, it implies how to swing. He replied, perhaps a better title might have been “Optimizing the Contact”.
The purpose of this study is to compare a downward swing (with arc) colliding with a ball at 0° with offsets of 0.5 in. and 1.0 in., to an upward attack angle swing colliding with a ball at 17° with the same offsets. My intention is to explore alternative swing paths to achieve the same or close to the same objective as the professor’s: optimal flight distance of a batted ball.
This study will evaluate two different swing types, a downward swing and an upward-swing. It will demonstrate that two different swing types given a set of assumptions can produce a similar batted ball. I will also look at different offsets to demonstrate how important aim is to each swing type.
This study will not include many of the parameters existent in a batted ball event that arise from the physical contributions of a batter, such as efficiency or time of execution. A follow-up article to this one will consider these parameters and many more. Its focus will be the practical application of various swing theories. Perhaps then, a batter can conclude what swing is optimal for their individual skill-set and objective.
It should be noted that models and data from Professor Nathan’s publications were used for this evaluation. This study will use the same models detailed in “Optimizing the Swing” and “Optimizing the Swing, Part Deux: Paying Homage to Teddy Ballgame”.
Batting Assumptions and Set Up
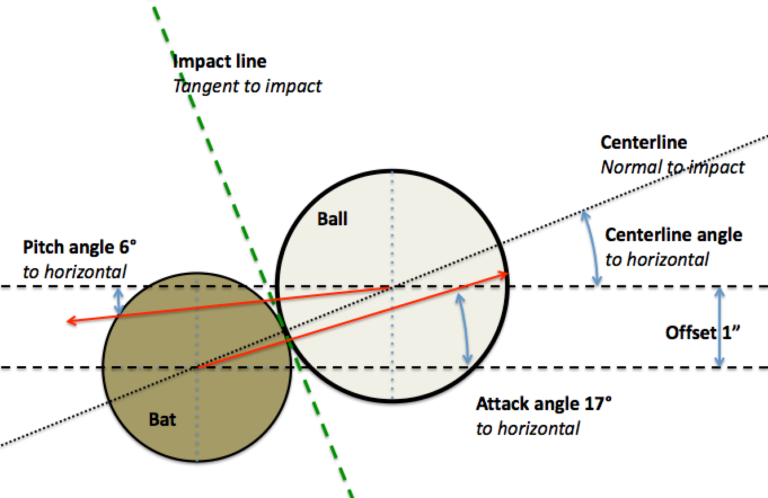
For this study I considered an 86 mph fastball with a backspin of 2000 rpm, and a descent angle of 6°. The batter is positioned so that during the swing, the bat collides with the ball when both are at the middle of the plate and at its front edge. This alignment will drive the ball to centerfield when the bat arrives at the ball with its barrel perpendicular to it [ball]. I assumed a fixed bat speed of 70 mph.
As mentioned previously I evaluated 2 different swing paths. The downward swing will produce an attack angle of 0° at impact. The upward-swing will produce an attack angle of 17° at impact. To expand the study for each swing path I evaluated two different offset values, 0.5” and 1.0”. This results in 4 cases to evaluate.
Test Case Evaluations
Each test case is evaluated below. In evaluating each test case a certain number of assumptions needed to be made. For several steps I interpolated values from contour plots or heat maps which leads to some inaccuracy in the numbers. As such, the number are not accurate but they can be used for qualitative evaluation.
First let’s visualize the 4 test cases.
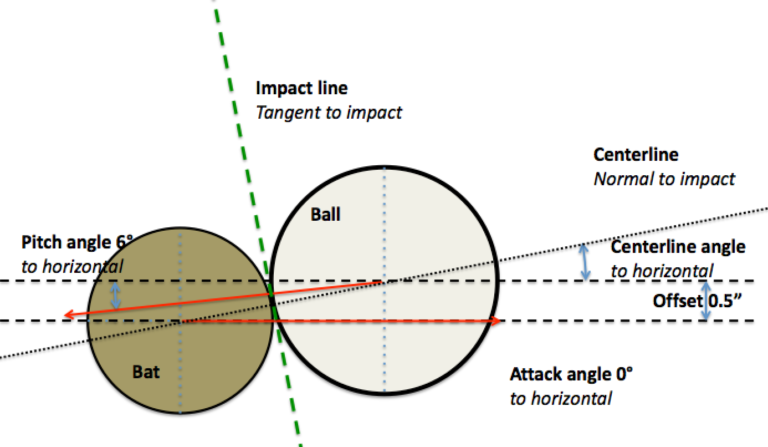
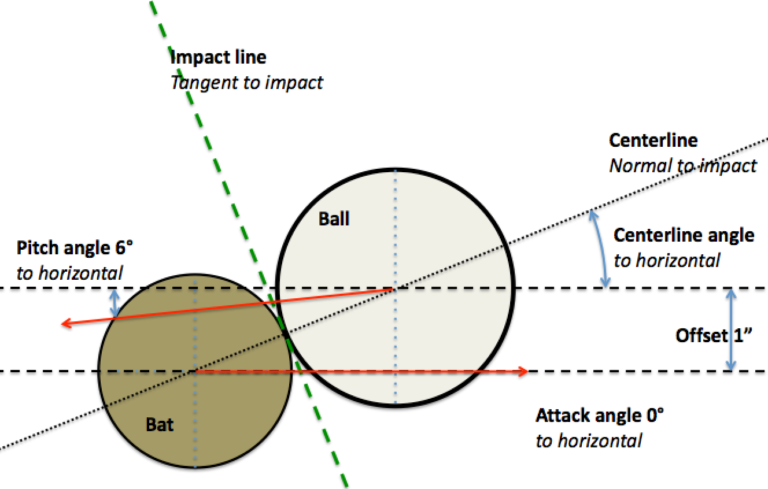
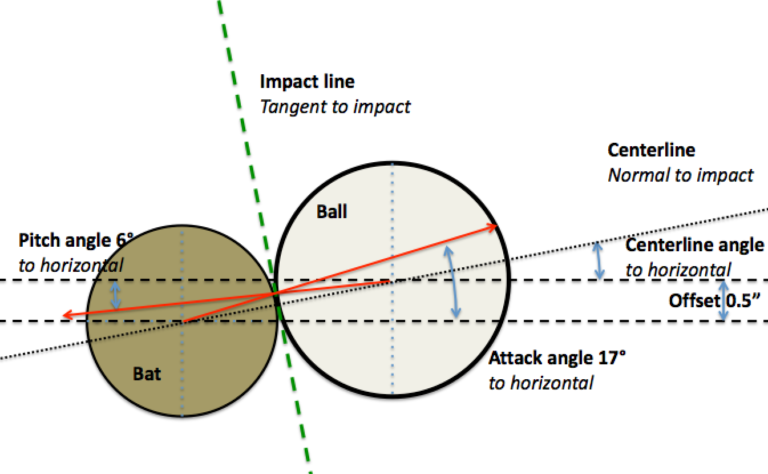
Note that the attack angle is larger than the centerline angle and the impact will lead to topspin.
First, the exit speeds and launch angles from the 4 combinations were determined from the attack angle and offset. In order to do this, I used the heat maps made available in “Optimizing the Swing, Part Deux: Paying Homage to Teddy Ballgame” by Prof. Nathan. Since I am getting values off of a heat map, the speeds and launch angle values are not exact.
- An attack angle of 0° with an offset of 0.5 in. produces an exit speed of 98 mph and a launch angle of 8°
- An attack angle of 0° with an offset of 1.0 in. produces an exit speed of 96 mph and a launch angle of 22°
- An attack angle of 17° with an offset of 0.5 in. produces an exit speed of 98 mph and a launch angle of 11°
- An attack angle of 17° with an offset of 1.0 in. produces an exit speed of 100 mph and a launch angle of 26°
Next I solved for backspin, which influences the flight of the ball. By using bat speed, attack angle, and offset, I calculated backspin using equations and constants from the publication “Oblique collisions of baseballs and softballs with a bat” by Kensrud, Nathan and Smith. The constants assumed in this step align with a specific baseball hit with a specific wooden bat.
- An exit speed 98 mph, attack angle of 0° and 0.5 inch offset produces ~1225 rpm of backspin.
- An exit speed 96 mph, attack angle of 0° and 1.0 inch offset produces ~ 2325 rpm of backspin.
- An exit speed 98 mph, attack angle of 17° and 0.5 inch offset produces ~ 675 rpm of topspin.
- An exit speed 100 mph, attack angle of 17°and 1.0 inch offset produces ~ 470 rpm of backspin.
Finally I used the flight path calculator Professor Nathan published on his website, http://baseball.physics.illinois.edu. With exit speed, launch angle and backspin, the flight paths can be calculated and total distance can be recorded.
- Exit speed 98 mph, 1225 rpm of backspin, launch angle of 8° results in ~ 250 ft. of distance
- Exit speed 96 mph, 2325 rpm of backspin, launch angle of 22° results in ~ 370 ft. of distance
- Exit speed 98 mph, 675 rpm of topspin, launch angle of 11° results in ~ 170 ft. of distance
- Exit speed 100 mph, 470 rpm of backspin, launch angle of 26° results in ~ 360 ft. of distance
Conclusion
Based on the total distances for each swing type, one can conclude that a hitter can hit a pitch just about as far with a 0° angle of attack and a 17° angle of attack if you have an offset of 1.0 inch. These distances show that the downward swing and the upward-swing are similarly effective swing types given the same speed and timing. If that hitter misses by half an inch, a 0° attack angle swing will hit the ball about 80 feet farther than a 17° attack angle swing.
My next article will address how to apply known and practiced swing philosophies to execute these conclusions. I will discuss margin for error, how hand/eye coordination (as well as it can be explained) applies, and other factors contributing to attaining specific objectives. Bat speed, the production of, is foremost, and will be considered, along with the batters aim. Also, I will prove how a downward-swing will hit a baseball exactly the same distance as an upswing when comparisons are made using pitches on the inner portion of the plate.
Please send questions and comments to:
