Explaining Professor Alan Nathan’s Optimal Attack Angle Swing, How It Is Not Optimal
and Its Misinterpretation
By Ken Cherryhomes
Introduction
Had Professor Nathan called his swing theory something other than the “optimal” attack angle, and had he not chosen a pitch over the middle of the plate hit to centerfield for his test study, I may not have written this article. His science and conclusions are sound, in a vacuum. Outside of the vacuum, all swings are not straight lines, and all bat speeds are not equal. Likewise, neither are all pitch locations.
Too many analytics are focused on outcome, without consideration for the methods or means to achieve or improve upon them. A hitting paradigm is being built on science. But is this science being interpreted and applied correctly, and are hitters suffering the consequences as a result of the inefficiencies of the methods aimed at achieving specific objectives?
Professor Nathan’s study discusses the optimal result of a bat/ball collision, but not the method or means (the swing) to achieve this objective optimally.
Optimal is a word, when assigned to anything, implies all things have been considered, weighed, measured and tested. Even in a vacuum, the attack angle he, and much of baseball, brands optimal, is not.
I agree that Professor Nathan’s study and conclusions, specifying the optimal swing angle for the optimal launch angle & exit velocity of a baseball are 100% valid outside the vacuum – when applied to an inside pitch, but the assignment of optimal to a swing path can be easily misunderstood.
In a vacuum, exists the luxury of including some, but not all, variables, and is where constants can be chosen. Sometimes, the narrative can direct the findings.
I struggled most with his study, as a hitting coach, with the application of his conclusions outside the vacuum, because of the parameters that were not included. The purpose of his study was to illustrate the best method to achieve a specific objective, and Professor Nathan did exactly that. Only not the way you think he did, and not with a pitch over the middle of the plate.
I will expand the scope of his study by including the parameters Professor Nathan left out, and discuss the application of Professor Nathan’s hypothesis. I will use his original models and diagram, as well as a few of my own, to demonstrate his points and mine. I intend to prove my theory that a more efficient, “natural” swing is optimal, and I will provide the science to back it.
Professor Alan Nathan’s study
The professor’s study, “Optimizing the Swing”, was first published by The Hard Ball Times, November 11, 2015. I am including his original diagram along with a paraphrased description to set up the conditions for this discussion, and to show the professor’s work and findings.
Test set up
A ball is positioned on a batting tee, 3.0 ft. above the ground, situated at the middle front edge of the plate, aligned with second base and center field. The bat being swung is at a fixed speed of 70 mph. The directional flight of the ball will be centerfield.
Now, before I move on to his diagram, I’m not sure if his experiments were performed on paper or if they included an actual ball and bat (NASA flew men to the moon on paper, successfully, before they actually flew to the moon), so I am going to provide a few more details to help explain how a bat would collide with the ball in its fixed position over the middle of the plate, and drive it to centerfield.
Simply because a ball is over the middle of the plate, doesn’t mean it will go to centerfield when struck. The batter’s orientation in the batter’s box and their proximity to the ball play key roles in this accomplishment. For the ball to travel in a straight line to centerfield with maximum force, the barrel of the bat (its vibrational node, or “sweet spot “) should arrive at roughly 90° from its starting point, perpendicular to the ball. Here, the ball should be in a position just in front of the batter’s little toe. Imagining an average size batter, they would be approximately 3.0 ft. away from the center of the plate, hands/arms at near full extension, forward. This may seem superfluous now, but it comes to bear further on in this discussion.
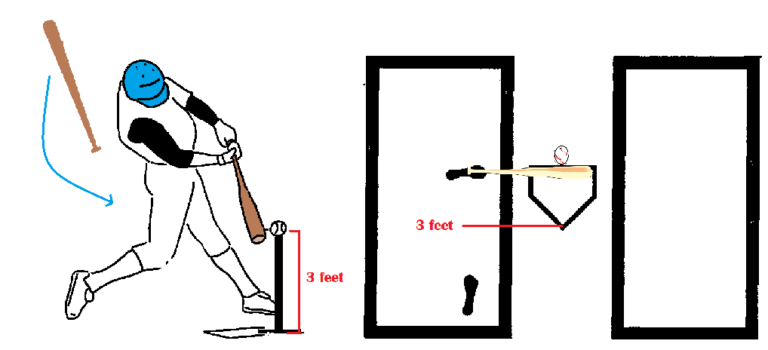
Professor Nathan’s optimal attack angle
Below is the diagram provided by Professor Nathan that explains the dynamics involved in his hypothesis.
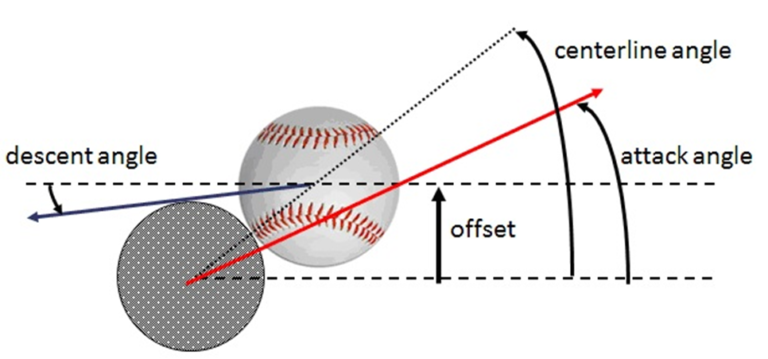
The centerline is the dotted line connecting the center of the bat to the center of the ball. The centerline angle is the angle the centerline makes with the horizontal. The offset, in Professor Nathan’s diagram, is one of two parameters under the batter’s control that characterize the swing. The offset is the measure of the batter’s aim and it determines the centerline angle. The second parameter is the attack angle. This is the relationship between the attack angle of the bat, the descent angle of the ball, and the centerline, all playing key roles in the resulting flight of the batted ball.
Professor Nathan asserts, if a batter’s desire were to hit a ball as far as possible, swinging down on the ball with a negative attack angle, that which is not aligned with the descent angle of the ball, “does not appear to be a good idea”. My first thought was, this would be true, assuming all attack angles stay their course, i.e., a downward swing path had no arc or change in direction when affected upon by human biomechanics.
Being a hitting coach, I had a difficult time wrapping my brain around the notion that an attack angle traveling upward towards a pitch oriented to fly to centerfield, was optimal. I had to disregard my definition of “optimal”, which includes all sorts of parameters such as efficiency and alternative offsets… and simply stick to the science presented. Professor Nathan’s assumptions are, after all, just stating his conclusion for an optimal attack angle at the instantaneous point of contact.
I returned to Professor Nathan’s diagram, and with a little help from my business partner, who works as a nuclear engineer, began to understand why and how Professor Nathan arrived at his conclusion.
My question was this: abandoning any mechanical argument as to the efficiency of the act, how can a bat traveling upward, making contact at a specific point with a ball, produce more flight distance than a ball struck by a bat arriving from above and then through (a typical swing arc) the ball, colliding with it at the exact same point with the exact same bat speed?
My understanding of how exit velocity is produced for a stationary ball hit by a bat is, it’s dependent on two things: the weight of the bat and the speed the bat is traveling. To produce the greatest distance of travel required a launch angle, and I knew a number of ways to create offsets to achieve this, such as an offset produced by a round bat meeting a round ball below the center of the ball (see illustration below).
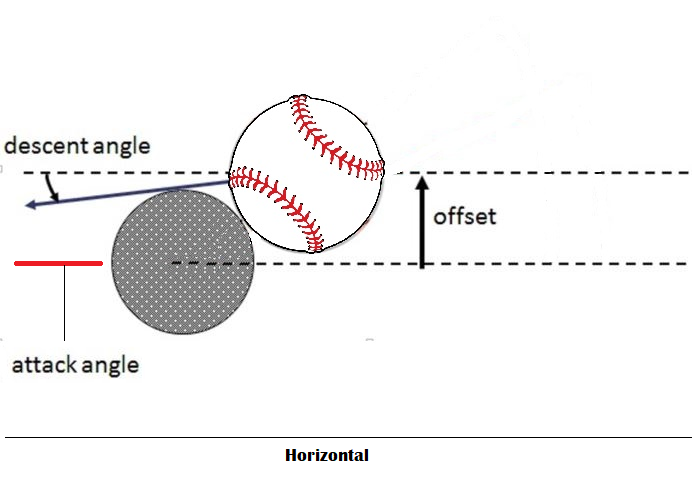
What I did not consider was the portion of the bat’s speed that does not act along the centerline. In an impact, the velocity of both the ball and the bat are decomposed to the portions that act tangential to the impact and normal to the impact. Portions of the velocity for each item that act normal to the impact have the largest influence on the exit velocity of the ball. As the attack angle shifts from the optimum specified by Professor Nathan’s study to a lower angle, let’s say of zero (as shown above), the portion of the bat’s speed that contributes to the ball exit velocity lessens due to the geometry of the impact, the conservation of momentum and the inefficiencies of the impact. The bat basically goes from a direct hit to a glancing hit, with the exit speed and launch angle changing as a result.
So, with the matter settled pertaining to the optimal angle of attack producing maximum flight distance of a ball in a vacuum, I’ll move to another discussion, the implementation of Professor Nathan’s assertions.
The implementation of a theory
Now that I understand how Professor Nathan arrived at his conclusions, I will discuss what is being done with them, and how attack angle is being implemented in games.
Numbers don’t lie. Conclusions, derived by solid, proven science, become practice, if the conclusions support a narrative. For the quantitative analyst, the game of baseball begins after the game is played. However, efficiency and how it contributes to the swing of a bat is not part of the analytics. Data points to objectives.
But baseball is a high stakes game, and because more often than not, the numbers are correct, more than ever before, numbers are part of the game. My job, as a hitting coach, has been to help players improve their analytics. I train them to be the best hitter they can be, exploiting their strengths, and strengthening their weaknesses. That was about as close a relationship I thought I would have with analytics.
Now there’s the attack angle swing, considered the optimal method to produce the optimal launch angle for maximum distance of a batted ball. The analytics confirm, while the least successful, most frequently occurring batted ball event, a fly ball produces more runs than a ground ball.
What the analytics do not consider is the other important parameters not taken into account in the study that concluded optimal attack angle, and how they apply to implementing this proven science of attack angle theory. Some pretty ridiculous batting drills started popping up on the sites of swing sensor providers. Once I realized that many of the metrics they assigned to swing characteristics were biased towards this swing theory, I then understood why these drills were posted.
More and more, I saw hitters with looping swings. The best hitters weren’t looping, guys like Mike Trout, who stated he swung down on the ball, but a crop of young, supremely talented players were, as it appeared to the eyes of this hitting coach and former scout. I had come to recognize this swing as the attack angle swing. The mechanical representation, called, “staying connected”.
The numbers, they may not lie, but they don’t explain how to achieve the optimal launch angle efficiently, or effectively, they just know what probably will happen when it occurs.
I didn’t read anywhere, Professor Nathan stating how to mechanically implement an attack angle swing. His study arrived at a conclusion of an instantaneous action, a bat hitting a ball. His test study, with its pitch over the middle of the plate – that is what has led to the confusion, resulting in ”connected” swings, inefficient mechanics, swing trackers biases, and a lot of bad instructional videos and coaching.
As this article progresses, I will explain how to mechanically achieve optimal launch angle exactly how Professor Nathan’s study suggests, by the most efficient means, considering all the variables absent from his study. I’ll also explain how an alternative swing path can achieve the same objective as the attack angle swing more efficiently – on a middle pitch.
Swing planes
Before I begin my study, including the variables absent from Professor Nathan’s study model, I would like to discuss swing paths and their efficiency. The word efficiency is at the core of my definition of optimal. Efficiency implies ease of execution, consistency achieving a desired objective, potential bat speed generated by a more “positive” attack angle, and since swinging a bat at a moving pitch involves time, time of execution.
There are three basic swing path theories implemented in the games of baseball and softball. There is the down swing, or what I will be referring to as the “natural” swing, the level swing, in its classic definition, horizontal to the ground and flat to the incoming pitch, similar to an “L” shape, and there’s the uppercut swing, newly refined and referred to as, the attack angle swing.
The “natural” down and through swing
The “natural” swing, or what has been referred to as a “down” swing, isn’t really a “down” swing at all, and contrary to what I have seen and heard taught by some hitting instructors, is not meant to collide with the ball while the bat is traveling along the downward plane of its arc.
Let me explain what I mean by “natural”, first. Imagine you want to reach for a glass of water. Your hand is at chest height, the glass is one foot below your hand, one foot in front of you. The glass is obviously within the scope of your reach in this scenario. At no time would your brain think it logical or efficient to lower your hand to the height of the glass, first, in line with the glass, then proceed forward to grasp it, giving the appearance of a level swing. The logical, natural path, would be a direct line to the glass. So, “natural”, first means intuitive1. It isn’t exceptional hand/eye coordination that makes a great hitter. We all have fine hand/eye coordination. What is not innate, is superior depth perception, the ability to process information at almost hyper-speeds, and a superior capacity to repeat learned synchronous motor functions, to name a few.
The “natural” downward swing has an arc shape to it. It travels in a direct path to the ball, beginning with the hitter’s hands position back, towards the back point of the rear shoulder and somewhere above the height of the strike zone. Once launched, the bat travels down/forward, level/forward, then up/forward, similar to a swing set you would find at your local park, but not quite as rounded an arc as a swing set.
The “natural” down swing is intuitive, direct, effort efficient (once the hitter begins the bat’s motion forward with a hard thrust, the bat no longer requires assistance to continue forward), and time efficient, due to its directness. Line drives, fly balls (home runs) and ground balls can all be achieved employing the “natural” downward swing.
Aside from the intuitive logic of a direct, “natural” swing path, another benefit is, it doesn’t have to be taught. Polished, yes, but not necessarily taught. Unless there are some limitations present (physical or brain related), hands go where eyes look when ordered to do so (few of us miss while reaching for our glass, if fully present and looking at the glass). So, suffice it to say, a bat being held in the hands of a batter can easily be directed to a stationary ball if the batter doesn’t intervene physically (attempts to control the act), disrupting the process by changing the bat’s course. The same is true with a moving pitch, so long as the swing is timed properly.
1If you search YouTube, you will find dozens of videos of toddlers hitting balls with bats. Take careful notice of the swing paths of these toddler sluggers, because it is a natural one. They haven’t yet been taught out of a natural swing.
The level swing
Someone had the idea that the method needed changing, when they decided they needed to control the exit vector of a ball struck by the bat2. For many hitters, the optimal launch angle (the directional travel of the ball after the bat/ball collision) was a line drive. Statistically, while the least occurring outcome of a bat/ball collision in the Major Leagues, the line drive results in a safe hit 69% of the time, a far greater success ratio when compared to ground balls, at 24%, or fly balls, just 21% of the time.
And so was born the level swing. As a hitting coach, I see it shaped like the letter “L”, and what bothers me most about this approach, is its inefficiency. Aside from its counter-intuitive indirectness (which is also time-inefficient), once the hands are lowered to the height of the ball, before progressing forward, a continued assistance (effort) is required to propel the bat forward from this position, which often causes the chest and head of the hitter, along with their bat, to pull off their intended swing path (don’t pull your head!). A visual description of this would be, a connection of the hips, chest and head of the hitter, all traveling together. The bat, hips, arms and chest of the batter become one, with the end of the bat (along with the chest and head) pointing somewhere around the dugout, at full extension. All variety of hits can be realized utilizing this method of swing, but due to its loss of torque assistance when the hands are lowered and because the bat travels a resistant plane, not a lot of bat speed is generated. And, there’s also the breakdown of the mechanics. You will find this is a similar description of what occurs with the “connected” swing, discussed below.
2The attempt to control the outcome of a batted ball, is likely the result of poor, but well-intended, advice from a coach.
The uppercut and or attack angle swing
This swing was popular with the kids. If they hit the ball, an impressive home run could result. As they got older, if they continued the practice, curveballs would drop onto their barrels for the occasional home run, but fastballs would blow by them. The loop of the uppercut took longer to get to the strike zone than the fastball took getting to the catcher’s mitt.
The uppercut, and by proxy, its refined counterpart, the attack angle swing, is usually performed by first dropping the back shoulder, in order to align the hands and bat of the hitter towards an upward swing path. With the attack angle swing, I’ve noticed something new. What I thought was a mechanical breakdown, the chest of the hitter flying open, is actually a practiced mechanic, the idea being, use the chest to compensate for the difficult approach angle of the swing and to aid in the generation of speed. It is called being “connected”. The connected attack angle swing appears to me to have difficulty remaining forward due to the chest/arm connection mechanics usually performed to execute it. The connected swing, as it is called, requires the hands/arms and chest of the hitter to basically work in unison. Meaning, they act as a single unit. As the chest rotates, the hands and arms travel parallel to its rotation. Full extension of the hands/arms occurs when the chest is directed towards the dugout instead of forward, towards the pitcher. This is apparently done to create the attack angle swing on pitches where ordinarily the hands and arms would guide the bat. A very inefficient method. This connected swing, as described to me, supposedly takes advantage of the bigger, stronger muscles in the upper body. Note: The largest, gross muscle in our body is the gluteus maximus, further confounding this theory.
Why no one lowers their hands, like Ted Williams did, (creator of the matching planes theory on which Professor Nathan’s optimal attack angle swing is based) instead of dropping down to launch, I have no idea.
In any case, this swing path is more inefficient than the level swing. It takes more time to perform than a “natural” swing. It travels through a more resistant plane than even the level swing, requiring a sustained use of energy to execute, and, it’s far less forgiving to error & less likely to result in a line drive. The potential for mechanical breakdown due to the necessary sustained effort to keep it moving, along with its path of resistance, forces me to brand it the least efficient of the three swing planes.
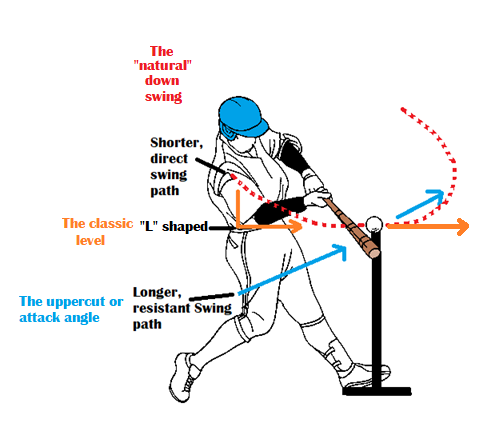
Next, I will discuss the various components that comprise an optimal swing. To do this, I’ll be applying these assumptions to a moving pitch.
Bat speed
In expanding the examination of optimal, bat speed must be addressed. Although I have not performed any tests to confirm this theory, I am confident a bat traveling downward would generate more speed than a bat traveling upward. In Professor Nathan’s model, all bats traveled 70 mph, regardless. If the baseline is 70 mph for a swing traveling through a greater plane of resistance, then in the same batter’s hands, the bat would travel faster while traveling a less resistant path. This seems academic. I have set up a challenge later on in this article that could resolve this argument.
Consistency
From the breakdown of swing paths due to sustained efforts, to an analytics born philosophy aimed at producing fly balls, and diminishing ground balls, consistency of outcome (a positive one) is also affected by the attack angle swing theory’s employment. Margin for error should also be considered, as this too, plays a role in consistency (Professor Nathan mentions this in his article). A “natural” downward path can produce a ground ball, fly ball, or line drive. Miss-hit attack angle swings, are more likely to produce pop ups, fly outs, and topspin ground balls. While I do not have access to the StatCast data, and a longer span of time is required to make an accurate assessment, logic, reason, and experience compel me to believe the line drive hit with any positive backspin’s frequency would be diminished, by implementing an upward angle swing philosophy (line drives with backspin continue to rise and often result in home runs). Based on Professor Nathan’s diagram, it is far more likely most line drives hit by an upward traveling bat would be one with topspin, not backspin. Many of those topspin collisions would result in…ground balls. What we are seeing from attack angle hitters is more strike outs. As a hitting coach, I would guess some of these strike outs we are seeing from attack angle swingers can be attributed to the time it takes to perform these swings. And, as I stated earlier, the sustained effort & subsequent breakdown of the intended path also contributes to many of those strike outs.
Time of execution
In this discussion, I won’t even bother testing or comparing the classic level swing, because virtually no one in professional baseball employs this method (Ty Cobb did against Walter ‘the train” Johnson). It’s interesting, because I ranked the upper cut swing below the classic level swing in terms of efficiency, but the bat speed & power that can be generated by an uppercut swing gives it an edge.
Time. Professor Nathan mentions in his study he did not include this parameter, and for the purpose of determining optimal attack angle to achieve optimal launch angle, it wouldn’t apply. In my attempt to determine the optimal method of, not only launch angle, but overall an optimal swing, the time to execute a swing from launch to contact, must be considered.
By my estimation, the most efficient swing is the one that does the most damage, consistently, with the shortest swing. The path of a swing isn’t the only thing that takes time. Getting into the desired swing path also consumes time. Ideally, the position from which the bat starts, at its launch, draws a direct line to the intended target, the ball. Because of the arc shape of the “natural” swing I previously described, this is the case with the “natural” swing. It’s intuitive, direct and capable of generating more speed than the attack angle swing, because of its path of least resistance. The attack angle swing, as it is performed by most, requires a lowering, somehow, of the hands (described earlier). This usually appears as a drop of the back shoulder, to put the bat in line with the oncoming pitch’s angle of descent. The reason this bears repeating is I am going to illustrate how much time is consumed by this process. Note: Ted Williams, correctly, started his hands low, not having to lower them pre-attack. He maintained a direct path to achieve his objective while creating a level (to the ball’s descent) path.
To demonstrate this, I tested three college hitters. Of the three, Player X was the only one with an attack angle swing. Player X would drop his back shoulder before launching his bat at an upward angle, towards the incoming pitch. Players Y and Z both took “natural” angle swings. Utilizing a swing tracker I designed (no one made one that captured the metrics I needed, and yes, I have patented it), I captured forward motion swing times. Along with the swing tracker, I used a system I developed to capture and separate their forward motion swings from their reaction times and mechanics (part of my patent) such as Player X’s drop into his launch angle swing plane. I then subtract .180 from the total swing time of each hitter in this sample, which is an average reaction time for an athlete (I collect reaction times as well as swing times for other purposes, unrelated to this study). Each hitter took 5 swings on a batting tee, and another 5 swings on machine pitched balls. The hitters performed 5 sets of each. Their swings were then averaged for the results below.
Forward Motion Swing Time Total Swing Time (reaction time not included)
Player X .138 seconds .310 seconds
Player Y .144 seconds .252 seconds
Player Z .175 seconds .236 seconds
While Player X produced the quickest forward motion swing time, his overall swing time was slowest, due to his shoulder drop mechanics required to perform his attack angle swing. His swing time was impacted by his drop by .172 seconds, which translates to 21.59 ft. of ball travel at 90 mph (average of 85.59 mph over distance). This extra time to perform a drop, pre-launch, is often the difference between hitting and not hitting a pitch. When you factor in reaction time, the impulse that begins the swing, his swing time is .490, which means, in order to hit a 90 mph pitch, Player X would have to begin swinging when the ball is 61.51 ft. away. This tells us Player X is incapable of hitting a 90 mph pitch – unless the ball was thrown from somewhere behind the mound.
So, my recommendation is, while the attack angle swing will produce (on an inside pitch) greater launch distance, a swing designed solely to perform this task isn’t advisable for all pitch locations, or hitters (considering time), and it shouldn’t be one of multiple swings a hitter goes back and forth between3.
Exactly how much more distance does the attack angle swing produce, as compared to the “natural” swing?
Note: I found there was a negligible difference between time captures off the tee versus live balls, so I averaged the live ball swings, the tee swings, serving as warm up.
At this point, we were manually inputting some of the metrics, so you heard numbers being called out. I thought it was important to provide raw, unedited video of the system at work and the consistency of the swing results (other than an errant inside pitch).
Any pitch location can be programmed for hitting sessions. In this instance, we were working on a middle of the plate, belt high and below pitch. We could just as easily set up an inside or outside pitch and the Swing Alert™ would provide a signal for the hitter to pull or hit to the opposite field.
Addendum: The was an happy accident discovery during this testing session. Regardless if you buy into my timing system, despite independent research and studies of the spatial memory center of the brain in relation to deliberate practice, 11 of 12 of these swing, which were perfectly timed due to my Swing Alert
When working with a specific location, i.e., middle, in or out, the pitch velocity can be changed, faster or slower, and the Swing Alert™ will be delivered based on the pitch’s velocity. Using a programmable pitching machine that can sequence different pitch velocity and types, the hitter can practice perfect timing with multiple pitch velocities in a round of hitting.
In our third testing session, I invited out several hitters to test the system on. Towards the end of testing, I invited in a random 12-year-old to try the system. I asked his coach what the fastest pitcher he had ever hit against was throwing and he told me 65mph. I asked the boy if he’d like to hit a 90mph pitch and he said he’d like to try.
Because this 12-year-old was an untrained hitter, he didn’t have the best swing and he struggled getting his foot down to comfortably hit 90mph pitches. However, after I captured his decision to collision swing time, he was able to hit 90mph pitches, something he’d never come close to experiencing before. With a bit of work on his mechanics and stride timing, he would have been able to hit as cleanly and consistently as the other hitters in this session.
Here’s video from test session three, including the 12-year-old.
3This last suggestion will be addressed when I discuss pitch locations.
The distance challenge
To work this out, I’ll return to the vacuum to establish a new fixed component. I’ll use the former test model set up, ball on a tee, middle front edge of the plate, 3.0 ft. above the ground. The batter’s orientation in the batter’s box remains the same with the objective of driving the ball to centerfield upon collision with the bat.
The bat/ball collision setups, as described earlier: Professor Nathan’s matching bat ascent to the ball’s descent with its 1.0 in. offset. Compared to my alternative, “natural” downward swing, with its bat head colliding with the ball as it arrives at its level plane, with a 1.0 in. offset, producing the exact same launch angle as the attack angle swing.
I am changing one constant for this experiment. The fixed bat speed. Assuming the bat driving downward along its arc, through a less resistant plane, could generate 4.0 mph more velocity than a bat traveling along a more resistant plane (1.0 mph of bat speed = 1.2 mph of exit velocity = 6.0 ft. of distance). My conclusion is, a “natural” swing would generate 24 more feet of distance. So the same batter who generates 70 mph of bat speed with an attack angle swing would generate 74 mph of bat speed with a “natural” swing, in our experiment.
Evaluating the distance contour plots for a fastball that Professor Nathan provided in his study and selecting a similar offset, let’s say 1.0 in., a comparison can be made between two different attack angles. The optimum attack angle for this pitch and offset is roughly 17°. That attack angle would produce a ball hit roughly 405 ft. If instead, the attack angle were changed to 0°, which would be the angle for a “natural” swing colliding with the ball in Professor Nathan’s middle of the plate set up, the plot would produce a ball hit roughly 385 ft. The difference between the attack angle swing and the “natural” swing is roughly 20 ft., which can be made up with the efficiencies and increase of bat velocity of the “natural” swing, as previously described. Assuming there was a 4.0 mph increase (could be more, could be less) in bat speed for the “natural” swing, by creating another 24 ft. in distance (385 ft. + 24 ft.), this would result in the ball traveling 409 ft., compared to the 405 ft. of ball travel produced by the attack angle swing.
If someone wishes, they can determine by what magnitude gravity’s role in the production/reduction of bat speed plays, to arrive at a closer to exact bat speed difference between the two. Based on a quick calculation, 1.0 mph of bat velocity could be gained here, and the other 3.0 mph gained by virtue of the “natural” swing’s more mechanically efficient and less resistant path.fixed
Pitch location
Being the Boston Redsox fan and Ted Williams admirer Professor Nathan is, it would stand to reason he would be the physicist to prove the theory of the optimal swing angle for optimal launch angle of a batted ball. Ted Williams performed it to perfection. Professor Nathan’s theory of matching swing planes with pitch descent planes can be executed perfectly on pitches over the inner third of the plate. And, it can be done most efficiently by taking a “natural” swing.
Ted Williams’s theory of a slightly upward swing to create a level (to the ball) swing plane was and is correct. But, there is a problem with Teddy’s theory: he was a pull hitter. In an interview I saw, years ago, Ted spoke of his matching planes theory, when somewhere in the conversation he said something like, ‘but I was a pull hitter. Maybe if I used more of the field, I would have been a better hitter, I don’t know’. I would suggest, no, not necessarily, not based on his swing theory.
It isn’t a problem with the theory, it’s a problem with the application of the theory when it comes to hitting all pitches with an attack angle approach. Professor Nathan even went so far as to say, the attack angle swing is less forgiving than other approaches.
Pulling the ball, properly
This is where the science in Professor Nathan’s theory is absolutely accurate. Every hitter I have trained, I’ve taught to pull the ball, properly. I taught them to take the same swing on every pitch, down and through, with a “natural” arcing swing. Middle pitches, when timed correctly, are driven back up the middle, and if there is an offset present between the bat and ball, the ball rises, with backspin. If they want to increase the odds of an offset collision, I tell them to choose a bat that has the smallest barrel they can find (if I were Easton, I’d make an aluminum model with a 2 ½” barrel, not just the 2 ⅝” or 2 ¾” big barrels). To hit a ball to the opposite field, swing down and through, making contact around or just ahead of the belt buckle. But on a pitch over the middle third of the plate, pull it, and pull it properly.
Once the lower body rotation begins, engaging the core of the batter, the core and lats are fired, sending the bat down/forward, and once the bat is moving, the batter essentially releases it. The bat then follows its arc, down, below the ball. When the barrel is just beyond the 90° point of the swing, it naturally starts its whip. From here, the batter resist back with their hands, not pulling, but just equal to the force felt of the bat going forward; an opposite/equal reaction. The barrel is traveling at maximum speed & ascending at this point, just like Ted Williams said, and just like Professor Nathan has proven, up to meet the ball at its descent.
Pulling the ball correctly is extremely difficult. It is either learned or accidental. Those who have mastered the art, such as Ted Williams, Barry Bonds, Ken Griffey jr. and Mark McGwire, just to name a few, have enjoyed great success doing it. Why it is a learned practice, is because it confounds our hand/eye coordination when performed properly (this is the only pitch where the hands fall below the plane of the ball during the “natural” swing process).
First, the hitter needs to understand all pitches are not met at the same place. Yes, there is an inside, middle and outside pitch. However, a straight line is not drawn through these pitches, laterally, as far as contact points are concerned. The contact point shifts relative to the location of the bat’s sweet spot as it sweeps through the strike zone and the location of the pitch.
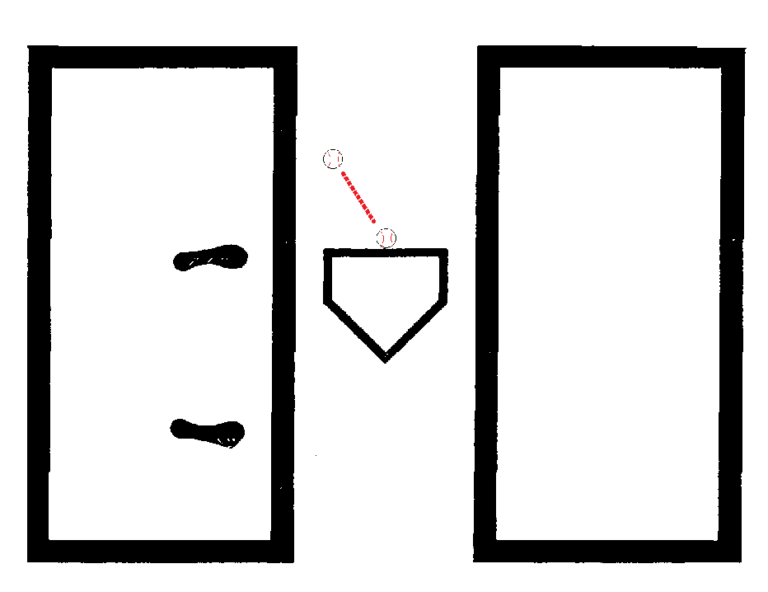
As I explained in our set up for Professor Nathan’s test, if our batter is oriented in the batter’s box so when his bat arrives at the ball on the batting tee at the front edge, middle of the plate, it arrives with the sweet spot of the barrel on the ball, perpendicular to it. This set up would drive the ball to center field. If we moved the batting tee to the inside front edge of the plate, the collision between the bat and ball would occur somewhere around the label of the bat, not the sweet spot. But if we move the batting tee, still over the inside of the plate, 1.0 ft. in front of the front edge of the plate (as depicted in the above diagram), the sweet spot of the barrel would collide with the ball, driving it to the batter’s pull field. On this pitch, the natural arc of the swing carries the barrel below the ball, then returns up, launching the ball into the air towards the batter’s pull field.
It doesn’t sound difficult, since you don’t have to drop down to achieve a conducive attack angle. But it is, because our eyes, correctly, communicate to our brain, mid-swing that our hands are no longer traveling towards the ball. Remember, our hands go where our eyes are looking, and our eyes are looking at the ball. What usually happens next is, the hitter “corrects” this assumed errant path by locking the front hand, readjusting the path to remain on course. The swing then catches the side, rather than the lower portion, of the ball. The mechanic often looks like a “chicken wing”. The barrel rolls over and the result is usually a ground ball to third or short. For this reason, pulling has been demonized for years.
If I can’t sing the praises of pulling the ball enough, the field is built disproportionate to the batter’s strength, proportionate to ease of execution. What I mean is, the batter’s pull field is the shortest distance required to hit a home run. When pulling a pitch, the greater distance of travel of the bat, along with its centrifugal whip, both aid in the generation of bat speed. Bat speed plus launch angle equals exit velocity, all executed optimally.
I suspect every hitter in the MLB can hit a ball 350 ft. If they were to pull a pitch over the middle third of the plate correctly, the ball would be hit out of almost every ballpark for a home run (see: Bucky Dent). The same cannot be said for all batters hitting to centerfield.
But because it is difficult, it is seldom done properly. I believe every hitter should be taught to pull properly. The problem is, I don’t think there are many coaches out there that agree with me, and even fewer who know how to teach it.
Conclusion
I believe I’ve demonstrated how a “natural” swing can equal or possibly exceed the maximum flight distance of a batted ball, as compared to Professor Nathan’s optimal attack angle swing. How much distance can be compensated for with a “natural” swing path, depends on the actual velocity increase of a bat traveling on a less resistant plane. Nevertheless, the ease of execution and intuitive qualities of the “natural” swing, along with its ability to achieve Professor Nathan’s optimal attack angle on pitches over the inner third of the plate, earns its distinction as a more optimal swing path.
My swing theory isn’t a new one, it’s an old, tried and true philosophy. It has been practiced for decades and is still in use at the Major League level today by many of the best hitters. Other than the learned lower body mechanics, it’s simple to perform. It’s natural. Over and over, swing theories have been complicated by the misapplication of science, from Charlie Lau’s transitional swing theory to the connected attack angle theory (not Professor Nathan’s doing). The answer has been there all along, in the hands of a toddler swinging a bat. It’s Occam’s razor.
I understand what Professor Nathan means by optimal attack angle. I understood what Ted Williams meant by a slightly upward swing. Still, I believe the term optimal, when it is assigned to anything, should come with a disclaimer. Equal weight must be given to ease of execution, efficiency and consistency.
Analytics driven objectives don’t consider everything. A hitter taking an approach with the intent to hit a line drive, if the hitter misses a little below the center of the ball, they have a possible double, maybe a home run. If they miss a little above the middle of the ball, a hard ground ball. Maybe that ground ball gets through for a hit. With the connected attack angle swing, as it is applied by many, more often than not, is all or nothing. Miss below, it’s a pop up or fly ball. Swing too early, a topspin grounder.
As a hitting coach, the “optimal” swing is the swing that works best for the individual. If the connected attack angle swing is producing favorable results, then that is the “optimal” swing for them. My job is to educate my hitters of the shortcomings and potential collateral damage of any swing approach they choose to utilize, and work with them to best optimize whatever that approach may be.
As for the analytics that led to the paradigm, analytics are meant to be used to observe trends, patterns, and change to predict outcomes, not for focusing on outcome objectives without consideration for the processes needed to achieve them. The players of the game of baseball are kids with dreams being realized. They deserve all the information they can get so they can continue living their dreams. It is our responsibility, the baseball community, to provide it. Discussions, debates and shared knowledge are our best tools to fulfill this obligation.
Any questions or comments can be sent to
